Fracții

Procente

Procentul este o fracție cu numitorul 100.

Exemple :

1% reprezintă o sutime:

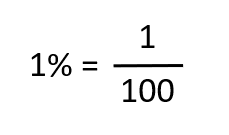
10% reprezintă o zecime:

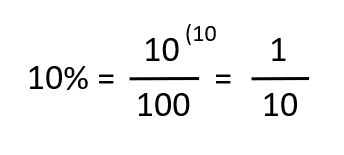
50% din ceva reprezintă jumătate din acea cantitate

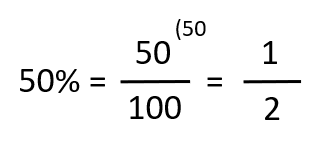
100% reprezintă un întreg

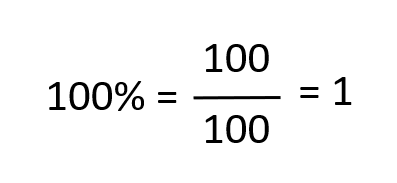
Pentru a afla un procent "p " dintr-un număr se înmulțește fracția 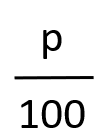cu acel număr.

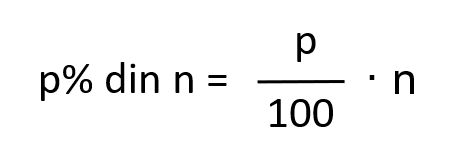
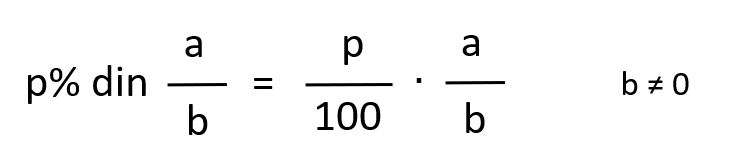
1. Un agricultor are 1 200 de kg de cartofi pe care vrea să le vândă. Un client vrea să cumpere 40% din cantitate, iar un alt cumpărător 60% din ce rămâne. Câți cartofi cumpără fiecare?

Rezolvare

40% · 1200 = \(\frac{40}{100}\) · 1200 = 480 kg cumpără primul client.
‎ 1200 – 480 = 720 kg mai rămân
‎ 60% · 720 = \(\frac{60}{100}\) · 720 = 432 kg cumpără al doilea client.

2. Să se calculeze 70% din 500 și 90 % din 400. Care dintre cele două numere este mai mare?

Rezolvare

70% · 500 = \(\frac{70}{100}\) · 500 = 350
‎ 90% · 400 = \(\frac{90}{100}\) · 400 = 360
‎ 350 < 360 deci
‎ 70% din 500 < 90% din 400

3. Pe un drum de munte ne este indicată o pantă de 10%. Acest număr reprezintă declivitatea drumului . Care este înălțimea care trebuie urcată dacă parcurgem 10 km pe acel drum? Panta de 10% înseamnă că urcăm 10m pentru 100m parcuși.

Rezolvare

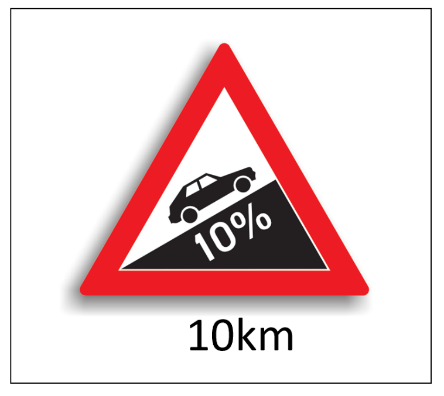
10% · 10 = \(\frac{10}{100}\) · 10 = 1. Înălțimea este de 1km sau de 1000m.
‎

4. Un tricou costă 120 lei dar la reducere Adina l-a cumpărat cu 90 lei.

Care este procendul de reducere aplicat de magazin?

Rezolvare

Reducerea este de 120 − 90 = 30 lei
‎ Ce procent reprezintă 30 lei din 120 lei?
‎ \(\frac{30}{120}\) · 100 = \(\frac{300}{12}\) = 25
‎ Reducerea a fost de 25%

5. Calculați:

a) 20% din 300 + 45% din 1200 + 10% din 130

b) 7% din 123 + 9% din 5 - 2% din 3

c) 32% din 660 - 15% din 360 - 58% din 110

Rezolvare

a) \(\frac{20}{100} · 300 + \frac{45}{100} · 1200 + \frac{10}{100} · 130\) = 20 · 3 + 45 · 12 + 1 · 13 = 60 + 540 + 13 = 613

b) \(\frac{7}{100} · 123 + \frac{9}{100} · 5 - \frac{2}{100} · 3\) = \(\frac{861}{100} + \frac{45}{100} - \frac{6}{100}\) =

= \(\frac{906}{100} + \frac{45}{100} - \frac{6}{100}\) = \(\frac{900}{100}\) = 9

c) \(\frac{32}{100} · 660 - \frac{15}{100} · 360 - \frac{58}{100} · 110\) = \(\frac{32}{10} · 66 - \frac{15}{10} · 36 - \frac{58}{100} · 11\) =

= \(\frac{2112}{10} - \frac{540}{10} - \frac{638}{10}\) = \(\frac{1572}{10} - \frac{638}{10}\) = \(\frac{934}{10}\)

6. Determinați x, știind că:

a) x% din 50 = 15

b) x% din 175 = 42

c) x% din 300 = 81

Rezolvare

Putem folosi metoda “produsul mezilor = produsul extremilor”:

a) \(\frac{x}{100} · 50 = \frac{x · 50}{100} = \frac{15}{1}\)

x · 50 · 1 = 100 · 15

x · 50 = 1500

x = 1500 : 50

x = 30

b) \(\frac{x}{100} · 175 = \frac{x · 175}{100} = \frac{42}{1}\)

x · 175 · 1 = 100 · 42

x · 175 = 4200

x = 4200 : 175

x = 24

c) \(\frac{x}{100} · 300 = \frac{x · 300}{100} = \frac{81}{1}\)

x · 300 · 1 = 100 · 81

x · 300 = 8100

x = 8100 : 300

x = 27

7. Un aspirator costă 580 de lei. Care va fi prețul lui, după aplicarea unei reduceri de 5%?

Rezolvare

\(\frac{5}{100} · 580 = \frac{5 · 58}{10} = \frac{290}{10} = 29\) (suma de bani cu care va fi redus aspiratorul)

580 - 29 = 551 lei (prețul aspiratorului după aplicarea reducerii)

8. O minge de fotbal costă 130 de lei. Cât ar costa mingea dacă:

a) s-ar scumpi cu 20%

b) s-ar ieftini cu 10%

Rezolvare

a) \(\frac{20}{100} · 130 = \frac{20 · 13}{10} = 2 · 13 = 26\)

130 + 26 = 156 lei (prețul mingii după creșterea prețului)

b) \(\frac{10}{100} · 130 = \frac{10 · 13}{10} = 13\)

130 - 13 = 117 lei (prețul mingii după ieftinire)

9. La un concert se vând în total 3200 de bilete de 3 categorii: 40% cu prețul de 15 lei, 35% cu prețul de 10 lei, iar restul cu 8 lei. Aflați suma totală încasată.

Rezolvare

\(\frac{40}{100} · 3200 = 40 · 32 = 1280\) (numărul de bilete cu prețul de 15 lei)

\(\frac{35}{100} · 3200 = 35 · 32 = 1120\) (numărul de bilete cu prețul de 10 lei)

3200 - (1280 + 1120) = 3200 - 2400 = 800 (numărul de bilete cu prețul de 8 lei)

1280 · 15 = 19200 lei

1120 · 10 = 11200 lei

800 · 8 = 6400 lei

Suma totală încasată:

19200 + 11200 + 6400 = 36800 lei

10. Calculați:

10% din [ 20% din (15% din 30000)] =?

Rezolvare

\(\frac{10}{100} · [\frac{20}{100} · (\frac{15}{100} · 30000)]\) =\(\frac{10}{100} · [\frac{20}{100} · (15 · 300)]\) =

=\(\frac{10}{100} · (\frac{20}{100} · 4500)\) =\(\frac{10}{100} · (20 · 45)\) =

=\(\frac{10}{100} · 900\) = 10 · 9 = 90