Fracții ordinare Adunarea și scăderea fracțiilor cu numitori diferiți
Selecție de lecții videoFracții
Adunarea și scăderea fracțiilor cu numitori diferiți
Pentru a aduna sau scădea fracții cu numitori diferiți acestea trebuie aduse la un numitor comun.
Să luăm adunarea
:
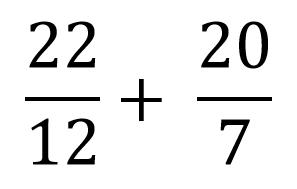
1. Se simplifică fracțiile până la forma ireductibilă .
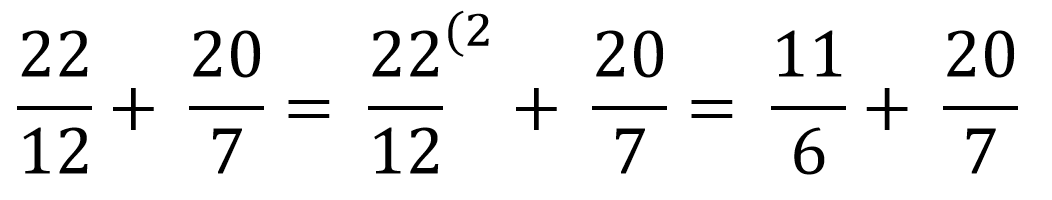
2. Se găsește numitorul comun care este cel mai mic multiplu comun dintre numitori.
cmmmc dintre 6 și 7 este 42
3. Se amplifică fiecare fracție cu câtul dintre cmmmc și numitorul fracției respective.
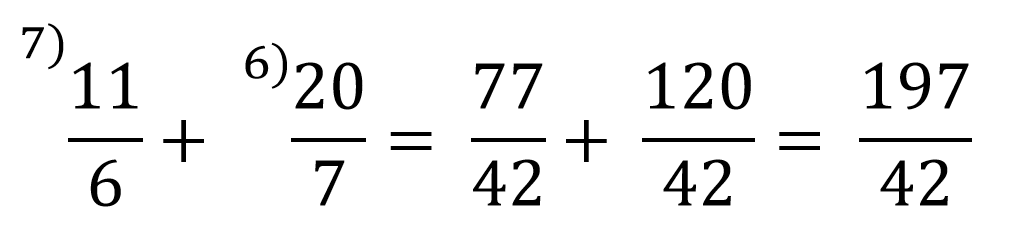
1. Calculați
2. Calculează \(\frac{15}{7} + \frac{15}{6}\) și \(\frac{5}{6} + \frac{4}{15}\) .
\(\frac{15}{7} + \frac{15}{6}\) = \(^{^{6)}}\frac{15}{7} + ^{^{7)}}\frac{15}{6}\) = \(\frac{90}{42} + \frac{105}{42}\) = \(\frac{195}{42}\)
\(\frac{5}{6} + \frac{4}{15}\) = \(^{^{5)}}\frac{5}{6} + ^{^{2)}}\frac{4}{15}\) = \(\frac{25}{30} + \frac{8}{30}\) = \({\frac{33}{30}}^{^{(3}}\) = \(\frac{11}{10}\)
3. Calculează și simplifică rezultatul, dacă este cazul: \(\frac{5}{6} – \frac{5}{15}\) = ?; \(\frac{14}{9} + \frac{8}{4}\) = ?
\(^{^{5)}}\frac{5}{6} – ^{^{2)}}\frac{5}{15} = \frac{25}{30} – \frac{10}{30} = \frac{15}{30}^{^{(15}} = \frac{1}{2}\);
\(^{^{4)}}\frac{14}{9} + ^{^{9)}}\frac{8}{4} = \frac{56}{36} + \frac{72}{36} = \frac{128}{36}^{^{(4}} = \frac{32}{9}\)
4. Calculează: \(\frac{14}{9} + \frac{8}{4} – \frac{1}{36} – \frac{8}{4}\) = ?
Numitorul comun este 36.
\(\frac{14}{9} + \frac{8}{4} – \frac{1}{36} – \frac{8}{4} = ^{^{4)}}\frac{14}{9} + \frac{1}{36} = \frac{56}{36} – \frac{1}{36} = \frac{55}{36}\)
5. Efectuează adunările aducând fracțiile la același numitor:
a) \(\frac{15}{7}+\frac{15}{6}\) =
b) \(\frac{5}{6}+\frac{4}{15}\) =
a) \(\frac{15}{7}+\frac{15}{6}\) = \(^{^{6)}}\frac{15}{7}+^{^{7)}}\frac{15}{6}\) = \(\frac{90}{42}+\frac{105}{42}\) = \(\frac{195}{42}\)
b) \(\frac{5}{6}+\frac{4}{15}\) = \(^{^{5)}}\frac{5}{6}+^{^{2)}}\frac{4}{15}\) = \(\frac{25}{30}+\frac{8}{30}\) = \({\frac{33}{30}}^{(3}\) = \(\frac{11}{10}\)
6. Efectuați adunările, amplificând doar una dintre fracții :
a) \(\frac{3}{15} + \frac{4}{3}\)
b) \(\frac{12}{7} + \frac{5}{21}\)
c) \(\frac{25}{6} + \frac{14}{18}\)
d) \(\frac{11}{52} + \frac{9}{13}\)
e) \(\frac{16}{23} + \frac{43}{115}\)
a) \(\frac{3}{15} + \frac{4}{3} = \frac{3}{15} + ^{^{5)}}\frac{4}{3} = \frac{3}{15} + \frac{20}{15} = \frac{23}{15}\)
b) \(\frac{12}{7} + \frac{5}{21} = ^{^{3)}}\frac{12}{7} + \frac{5}{21} = \frac{36}{21} + \frac{5}{21} = \frac{41}{21}\)
c) \(\frac{25}{6} + \frac{14}{18} = ^{^{3)}}\frac{25}{6} + \frac{14}{18} = \frac{75}{18} + \frac{14}{18} = \frac{89}{18}\)
d) \(\frac{11}{52} + \frac{9}{13} = \frac{11}{52} + ^{^{4)}}\frac{9}{13} = \frac{11}{52} + \frac{36}{52} = \frac{47}{15}\)
e) \(\frac{16}{23} + \frac{43}{115} = ^{^{5)}}\frac{16}{23} + \frac{43}{115} = \frac{80}{115} + \frac{43}{115} = \frac{123}{115}\)
7. Asociați convenabil termenii, apoi calculați :
a) \(\frac{11}{26} + \frac{9}{13} + \frac{15}{26} + \frac{4}{13}\)
b) \(\frac{41}{33} + \frac{5}{11} + \frac{10}{33} + \frac{2}{11}\)
c) \(\frac{5}{3} + \frac{17}{10} + \frac{19}{6} + \frac{23}{5}\)
d) \(\frac{11}{2} + \frac{17}{32} + \frac{5}{4} + \frac{6}{16}\)
a) \(\frac{11}{26} + \frac{9}{13} + \frac{15}{26} + \frac{4}{13} = \frac{11}{26} + \frac{15}{26} + \frac{9}{13} + \frac{4}{13} = \frac{26}{26} + \frac{13}{13}\) = 1 + 1 = 2
b) \(\frac{41}{33} + \frac{5}{11} + \frac{10}{33} + \frac{2}{11} = \frac{41}{33} + \frac{10}{33} + \frac{5}{11} + \frac{2}{11}\) =
= \(\frac{51}{33} + \frac{7}{11} = \frac{51}{33} + ^{^{3)}}\frac{7}{11} = \frac{51}{33} + \frac{21}{33} = \frac{72}{33}\)
c) \(\frac{5}{3} + \frac{17}{10} + \frac{19}{6} + \frac{23}{5} = \frac{5}{3} + \frac{19}{6} + \frac{17}{10} + \frac{23}{5}\) =
= \(^{^{2)}}\frac{5}{3} + \frac{19}{6} + \frac{17}{10} + ^{^{2)}}\frac{23}{5} = \frac{10}{6} + \frac{19}{6} + \frac{17}{10} + \frac{46}{10}\) =
= \(\frac{29}{6} + \frac{63}{10} = ^{^{5)}}\frac{29}{6} + ^{^{3)}}\frac{63}{10} = \frac{145}{30} + \frac{189}{30} = \frac{334}{30}\) =
= \(\frac{334}{30}^{^{(2}} = \frac{167}{15}\)
d) \(\frac{11}{2} + \frac{17}{32} + \frac{5}{4} + \frac{6}{16} = \frac{11}{2} + \frac{5}{4} + \frac{17}{32} + \frac{6}{16}\) =
= \(^{^{2)}}\frac{11}{2} + \frac{5}{4} + \frac{17}{32} + ^{^{2)}}\frac{6}{16} = \frac{22}{4} + \frac{5}{4} + \frac{17}{32} + \frac{12}{32}\) =
= \(\frac{27}{4} + \frac{29}{32} = ^{^{8)}}\frac{27}{4} + \frac{29}{32} = \frac{216}{32} + \frac{29}{32} = \frac{245}{32}\)
8. Mara a cheltuit \(\frac{3}{9}\) din toți banii ei pe cadoul pe care i l-a luat mamei ei de Crăciun, \(\frac{6}{18}\) pentru cadoul tatălui ei , iar de restul vrea sa își ia un cadou pentru ea. Câți bani din banii ei inițiali i-au mai rămas Marei pentru cadoul ei?
\(\frac{3}{9}^{^{(3}} = \frac{1}{3}\)
\(\frac{6}{18}^{^{(8}} = \frac{1}{3}\)
\(\frac{3}{3} – (\frac{1}{3} + \frac{1}{3}) = \frac{3}{3} – \frac{2}{3} = \frac{1}{3}\)
9. O bibliotecă cu cărți cântărește 24\(\frac{15}{8}\) kilograme, iar cărțile din ea cântăresc 12\(\frac{7}{10}\) kilograme. Câte kilograme cântărește biblioteca fără cărți în ea?
24\(\frac{15}{8}\) = \(\frac{207}{8}\)
12\(\frac{7}{10}\) = \(\frac{127}{10}\)
\(^{^{5)}}\frac{207}{8} - ^{^{4)}}\frac{127}{10} = \frac{1035}{40} - \frac{508}{40} = \frac{527}{40}\)
\(\frac{527}{40} = 13\frac{7}{40}\)
Chestionar
Puncte acumulate: 0 din 3
Care este răspunsul corect?
1. \(\frac{7}{4}\) + \(\frac{2}{3}\) =
Explicație
Vizibil doar după ce validați răspunsul.
Se aduce la același numitor: 12
\(\frac{7}{4} + \frac{2}{3} = \frac{7·3}{4·3} + \frac{2·4}{3·4} = \frac{21}{12} + \frac{8}{12} = \frac{29}{12}\)


