Fracții

Cel mai mare divizor comun (c.m.m.d.c)

Cel mai mare divizor comun a două numere naturale nenule este cel mai mare număr natural care divide cele două numere.

Notăm cel mai mare divizor comun al numelor naturale a și b cu

cmmdc dintre a și b

(a, b).

Exemplu:

cmmdc dintre 30 și 42 este 6 pentru că 30 = 6 · 5 și 43 = 6 · 7

(12 , 15) = 3 pentru că 12 = 6 · 2 și 15 = 6 · 3
‎ .

O fracție este ireductibilă dacă cel mai mare divizor comun dintre numitor și numărător este 1.

Exemplu:

\(\frac{28}{55}\) este ireductibilă pentru că 28 = 4 · 7 iar 35 = 5 · 11 deci cmmdc dintre 28 și 55 este 1 sau (28, 55) = 1

1. Aflați c.m.m.d.c. al numerelor 1440 și 2560 și apoi simplificați fracția \(\frac{1440}{2560}\) până la forma ireductibilă.

Rezolvare

‎ 1440 = 2 ⁵ · 3 ² · 5
‎ 2560 = 2 ⁹ · 5
‎ Pentru a afla cmmdc se iau factorii comuni cu exponentul cel mai mic: cmmdc al numerelor 1440 și 2560 = 2 ⁵ · 5 = 32 · 5 = 160
‎ Pentru a aduce fracția la forma ireductibilă simplificăm cu cel mai mare divizor comun dintre numărător și numitor.
‎ \({\frac{1440}{2560}}^{(160} = {\frac{9}{16}}\)

2. Demonstrați că 26 și 27 sunt prime între ele.

Rezolvare

26 = 13 · 2
‎ 27 = 3 ³
‎ Cum cele două numere nu au factori comuni mai mari decât 1, nu au divizori proprii comuni, rezultă că (26, 27) = 1, așadar cele două numere sunt prime între ele

3. Să se aducă fracțiile la forma ireductibilă: \(\frac{28}{35}; \frac{30}{42}; \frac{51}{45}\)

Rezolvare

\({\frac{28}{35}}^{(7} = \frac{4}{5}\) deoarece cel mai mare divizor comun al numerelor 28 și 35 este 7
‎ \({\frac{30}{42}}^{(6} = \frac{5}{7}\) deoarece (30, 42) = 6
‎ \({\frac{51}{45}}^{(3} = \frac{17}{15}\) deoarece (51, 45) = 3

4. Completați, fără a descompune în factori primi :

a) (12, 28) = ...

b) (16, 36) = ...

c) (100, 80) = ...

d) (15, 35) = ...

e) (14, 49) = ...

f) (35, 6) = ...

Rezolvare

a) (12, 28) = 4

b) (16, 36) = 4

c) (100, 80) = 20

d) (15, 35) = 3

e) (14, 49) = 7

f) (35, 6) = 1

5. Identificați perechile de numere prime între ele:

a) 12 și 9

b) 5 și 11

c) 15 și 27

d) 10 și 11

e) 20 și 72

f) 231 și 321

Rezolvare

a) (12, 9) = 3 ≠ 1, deci 12 și 9 nu sunt prime între ele

b) (5, 11) = 1, deci 5 și 11 sunt prime între ele

c) (15, 27) = 3 ≠ 1, deci 15 și 27 nu sunt prime între ele

d) (10, 11) = 1, deci 10 și 11 sunt prime între ele

e) (20, 72)

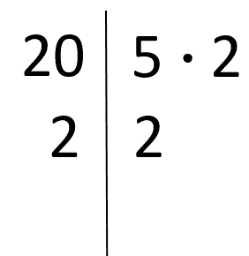
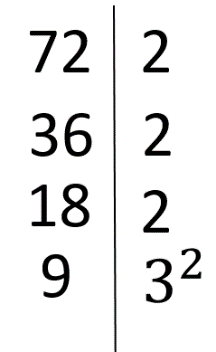
Deci (20, 72) = 2 ² ≠ 1, deci 20 și 72 nu sunt prime între ele

f) (231, 321)

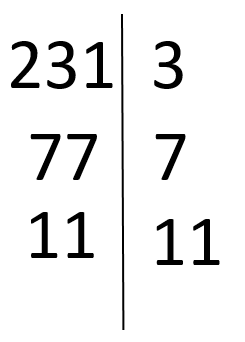
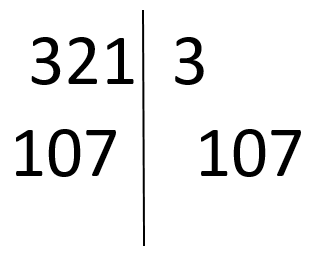
(231, 321) = 3 ≠ 1, deci 231 și 321 nu sunt prime între ele.

6. Simplificați următoarele fracții o singură dată pentru a ajunge la fracții ireductibile.

a) \(\frac{15}{45}\)

b) \(\frac{22}{33}\)

c) \(\frac{72}{56}\)

d) \(\frac{315}{135}\)

Rezolvare

a) (15, 45) = 15, deci trebuie să simplificăm cu 15

\({\frac{15}{45}}^{(15} = \frac{1}{3}\)

b) (22, 33) = 11, deci trebuie să simplificăm cu 11

\({\frac{22}{33}}^{(11} = \frac{2}{3}\)

c) (72, 56) = 8, deci trebuie să simplificăm cu 8

\({\frac{72}{56}}^{(8} = \frac{9}{7}\)

d) (315, 135) = 45, deci trebuie să simplificăm cu 45

\({\frac{315}{135}}^{(45} = \frac{7}{3}\)

7. Stabiliți varianta corectă de răspuns :

i) Divizorul comun dintre numerele 84 și 15 este :

a) 7 b)3 c)2 ² d) 5

ii) Cel mai mare divi zor comun dintre numerele 108 și 252 este :

a)2 ² · 3 b)3 ³ · 2 c)3 ² · 2 ² d)7 · 2 ²

Rezolvare

i) R ăspunsul corect este b)3

ii) Răspunsul corect este c) 3 ² · 2 ²

8. a) Scrieți divizorii comuni ai numerelor 12 și 18;

b) Scrieți cel mai mare divizor comun al numerelor 24 și 56;

c) Simplificați fracția \(\frac{28}{70}\) cu cel mai mare divizor comun dintre cele două numere;

Rezolvare

a) Divizorii comuni ai numerelor 12 și 18 sunt 2, 3 și 6.

b) (24, 56)

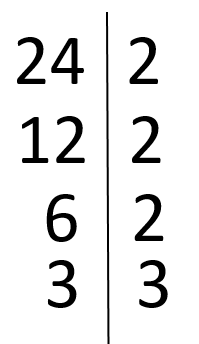
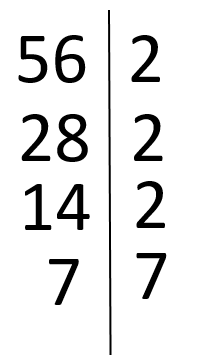
Deci (24, 56) = 2 ³

c) (28, 70)

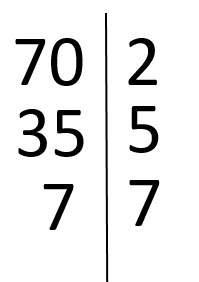
Deci (28, 70) = 2 · 7 = 14

\({\frac{28}{70}}^{(14} = \frac{2}{5}\)

9. Aflați cifra x, știind că cel mai mare divizor comun dintre 40 și 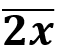este 5.

Rezolvare

Dacă (40, 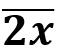) = 5, atunci 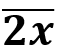se împarte la 5. Așa că, ne mai rămân două cazuri posibile: cazul în care x = 0, adică 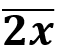= 20, și cazul în care x = 5, adică 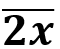= 25.

Să le verificăm pe rând. Dacă x = 0, atunci (40, 20) = 2 · 5 = 10. Deci am mai eliminat un caz, pentru că (40, 20) trebuia să fie egal cu 5.

Să verificăm și ultima noastră variantă, adică x = 5. (40, 25) = 5, deci am gasit cifra căutată.

10. Verificați următoarele propoziții, apoi scrieți in dreptul lor A daca sunt adevărate, și F dacă sunt false.

1. Cel mai mare divizor comun al numerelor 12 și 28 este 6 ;

2. Cel mai mare divizor comun dintre 45 și 72 este 3 ² ;

3. 19 este cel mai mare divizor comun al numerelor 19 și 57 ;

4. Cel mai mare divizor comun al numerelor 12, 18 si 30 este 12;

Rezolvare

1. F

2. A

3. A

4. F