Fracții ordinare Scoaterea întregilor din fracție
Selecție de lecții videoFracții
Scoaterea întregilor din fracție
Fiind dată o fracție supraunitară \(\frac{a}{b}\) cu b ≠ 0, putem afla câți întregi cuprinde această fracție. Spunem că am scos întregii din fracție.
De exemplu \(\frac{7}{2}\) conține 3 întregi pentru că 7
: 2 = 3 rest 1
Scriem:
\(\frac{7}{2}\) = 3\(\frac{1}{2}\)
Citim:
"trei întregi și \(\frac{1}{2}\)
Orice fracție supraunitară \(\frac{a}{b}\) poate fi scrisă sub forma c\(\frac{r}{b}\) unde fracția \(\frac{r}{b}\) este întotdeauna subunitară cu r,b ≠ 0.
Cum aflăm numerele c și r? Ele reprezintă câtul și restul împărțirii
:
a
: b = c rest: r
Exemplu:
\(\frac{23}{5}\) = 4\(\frac{3}{5}\) pentru că 23
: 5 = 4 rest 3
1. De câte mere întregi este nevoie pentru a tăia 43 de sferturi? Ce mai rămâne?
43 : 4 = 10 rest 3
\(\frac{43}{4} = 10{\frac{3}{4}}\)
Este nevoie de 11 mere
și ne rămâne un sfert în plus.
2. Scoateți întregii din fracție: \(\frac{13}{6}\); \(\frac{25}{7}\); \(\frac{73}{10}\); \(\frac{89}{13}\).
\(\frac{13}{6} = 2{\frac{1}{6}}\) pentru că 13
: 6 = 2 rest 1
\(\frac{25}{7} = 3{\frac{4}{7}}\)
\(\frac{73}{10} = 7{\frac{3}{10}}\)
\(\frac{89}{13} = 6{\frac{11}{13}}\);
3. Încadrează fracția \(\frac{23}{12}\) între două numere naturale consecutive, folosind scoaterea întregilor din fracție.
\({\frac{23}{12}} = 1{\frac{11}{12}}\)
deci \(\frac{23}{12}\)
este cuprinsă între 1 și 2 pentru că este un întreg + o fracție subunitară.
1 < \(\frac{23}{12}\) < 2
4. Copiați și completați liniile punctate pentru a obține o încadrare pentru fiecare dintre fracțiile propuse cu două numere întregi consecutive.
a) …<
\(\frac{16}{3}\)
< … b)
…<
\(\frac{27}{8}\)
<…
c)
…<
\(\frac{30}{7}\)
<… d)
…<
\(\frac{64}{5}\)
<…
Scoatem
întregii din fracții
:
a) 15
<
\(15\frac{1}{3}\)
< 16;
b) 3
<
\(3\frac{3}{8}\)
< 4
;
c) 28
<
\(28\frac{2}{7}\)
<
29
; d) 12
<
\(12\frac{1}{5}\)
<
13
5. Pentru fiecare axă plasați punctul indicat în dreapta scoțând în prelabil întregii din fracție. Observați și țineți cont de unitatea de măsură indicată de fiecare dată.
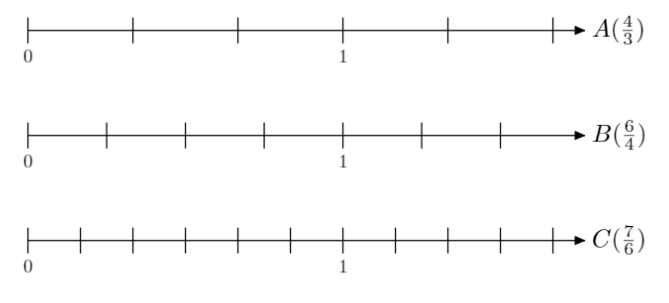
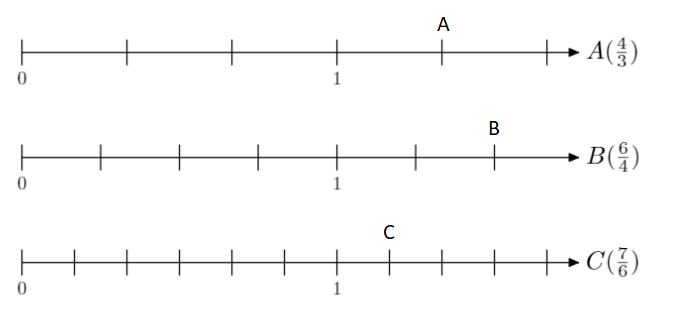
\(\frac{4}{3}\) = 1\(\frac{1}{3}\)
\(\frac{6}{4}\) = 1\(\frac{2}{4}\) = 1\(\frac{1}{2}\)
\(\frac{7}{6}\) = 1\(\frac{1}{6}\)
6. Scrieți fiecare fracție ca sumă a unui număr întreg și a unei fracții mai mică decât 1:
a) \(\frac{14}{9}\)
b) \(\frac{27}{5}\)
c) \(\frac{14}{3}\)
d) \(\frac{51}{8}\)
e) \(\frac{37}{4}\)
f) \(\frac{15}{7}\)
a) \(\frac{14}{9}\) = 1 + \(\frac{5}{9}\)
.
b) \(\frac{27}{5}\) = 5 + \(\frac{2}{5}\)
.
c) \(\frac{14}{3}\) = 4 + \(\frac{2}{3}\)
.
d) \(\frac{51}{8}\) = 6 + \(\frac{3}{8}\)
.
e) \(\frac{37}{4}\) = 9 + \(\frac{1}{4}\)
.
f) \(\frac{15}{7}\) = 2 + \(\frac{1}{7}\)
7. Scrie în căsuțele de mai jos A , dacă relațiile sunt adevărate, și F , dacă sunt false.
a) 7 < \(\frac{13}{2}\)

b) 3 > \(\frac{62}{30}\)

c) 9 <
\(\frac{79}{9}\)

d) 5 > \(\frac{199}{40}\)

a) F
b) A
c) A
d) F
8. Determinați numerele naturale consecutive între care se află fracția \(\frac{47}{13}\).
\(\frac{47}{13}\) = 3\(\frac{8}{13}\)
Deci 3 < 3\(\frac{8}{13}\) < 4
9. Completati spațiile libere cu <, = sau >, astfel încât să obțineți enunțuri adevărate:
a) \(\frac{13}{4}\) … 3\(\frac{3}{4}\)
b) \(\frac{17}{3}\) … 5\(\frac{2}{3}\)
c) 3\(\frac{4}{5}\) … \(\frac{23}{5}\)
d) 5\(\frac{3}{6}\) … \(\frac{25}{6}\)
a) \(\frac{13}{4}\) < 3\(\frac{3}{4}\)
b) \(\frac{17}{3}\) = 5\(\frac{2}{3}\)
c) 3\(\frac{4}{5}\) < \(\frac{23}{5}\)
d) 5\(\frac{3}{6}\) > \(\frac{25}{6}\)
10. Ioana are 50 de mere si vrea să le împartă egal celor 6 prieteni ai ei. Câte mere va avea fiecare prieten și cu câte mere va rămâne Ioana după împărțirea merelor?
\(\frac{50}{6}\) = 8\(\frac{2}{6}\)
Deci fiecare prieten va primi 8 mere, iar Ioana va rămâne cu 2 .

