Clasa a IV-a

Rezolvarea problemelor

Aflarea unui termen necunoscut

Aflarea unui termen necunoscut dintr-o operație de adunare
‎ a + 5 = 7
‎ Pentru a afla numărul a folosim proba adunării prin scădere:
‎ a = 7 – 5
‎ a = 2

Aflarea unui termen necunoscut dintr-o operație de scădere
‎ b – 10 = 15
‎ Pentru a afla numărul b folosim proba scăderii prin adunare:
‎ b = 15 + 10
‎ b = 25

14 – c = 10
‎ Pentru a-l afla pe "c" folosim proba sc ăderii prin scădere :
‎ c = 14 – 10
‎ c = 4

Aflarea unui termen necunoscut dintr-o operație de înmulțire
‎ d x 5 = 20
‎ Folosim proba înmulțirii prin împărțire :
‎ d = 20 : 5
‎ d = 4

Aflarea unui termen necunoscut dintr-o operație de împărțire
‎ e : 3 = 4
‎ Folosim proba împărțirii prin înmulțire :
‎ e = 4 x 3
‎ e = 12

15 : f = 5
‎ Folosim proba împărțirii prin împărțire
‎ f = 15 : 5
‎ f = 3

d : 4 = 5 rest 2
‎ Folosim proba împărțirii cu rest prin înmulțire și apoi adunăm restul la deîmpărțit :
‎ d = 4 x 5 + 2
‎ d = 22

1. Cât este jumătate din 1200?

Rezolvare

Pentru a afla jumătatea lui 1200, îl împărțim pe 1200 la 2:
‎ 1200 : 2 = 600

2. Află numul a dacă a + 4653 =6502.

Rezolvare

a = 6502 – 4653 = 1849

3. Un număr n este de trei ori mai mare decât 73. Care este numărul?

Rezolvare

n = 73 x 3
‎ 73x
‎ 3
‎ ____
‎ 219

4. În cadrul zilelor orașulu meu se organizează un concurs de ciclism pentru copii. Premiul total este de 320 de lei care trebuie repartizat primilor trei concurenți. Primul primește cu 70 de lei mai mult decât al doilea. Al treilea primește cu 80 de lei mai puțin decât al treilea. Ce premiu a luat fiecare din cei trei concurenți?

Rezolvare

Notăm sumele primite de cei trei concurenți cu a, b și c.
‎ Premiul total este de 320 de lei
‎ a + b + c = 320
‎ Primul primește cu 70 de lei mai mult decât al doilea.
‎ a = b + 70 Suma ne spune că trebuie să mai adăugăm 70 de lei la b pentru a fi egal cu a.
‎ Al treilea primește cu 80 de lei mai puțin decât al treilea.
‎ c + 80 = b Suma ne spune că trebuie să mai adăugăm 80 de lei la cel de-al treilea premiu (c) pentru a fi egal cu cel de-al doilea premiu (b).
‎ Î n suma celor trei premii a+b+c = 320 înlocuim premiul a cu b + 70 și premiul b cu c+ 80
‎
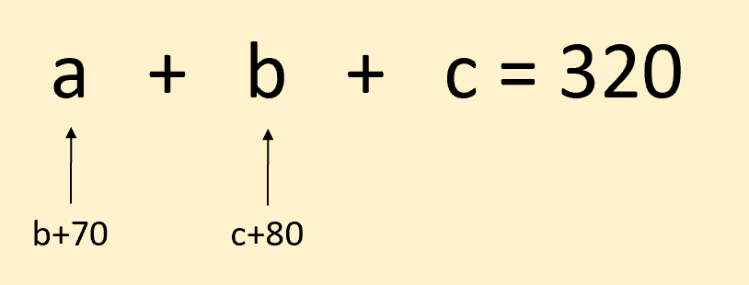
‎ (b + 70) + (c + 80) + c = 320
‎ Pentru că nu-l putem afla în același timp și pe b și pe c, mai înlocuim odată b = c + 80
‎ (c + 80) + 70 + (c + 80) + c = 320
‎ Desființăm parantezele pentru că adunarea este comutativă și asociativă.
‎ c + 80 + 70 + c + 80 + c = 320
‎ Reordonăm termenii numerici:
‎ c + c + c + 80 + 70 + 80 = 320
‎ Facem suma termenilor numerici
‎ c + c + c + 230 = 320
‎ Aplicăm metoda balanței și scădem 230 atât din partea stângă cât și din partea dreaptă
‎ c + c + c 230 – 230 = 320 – 230
‎ c + c + c = 320 – 230
‎ c + c + c = 90
‎ c = 30
‎ Pentru că b = c + 80 înseamnă că b = 30 + 80; b = 110
‎ Pentru c ă a = b + 70 înseamnă că a = 110 + 70 ; a = 180
‎ Facem proba
‎ a + b + c = 320
‎ 180 + 110 + 30 = 320

5. Bunica vrea să împartă nepoților câte 3 mere aurii, 5 mere roșii și 4 banane la fiecare. Știind că bunica are 3 nepoți, să se afle de câte fructe din fiecare tip are nevoie bunica.

Rezolvare

3 x 3 = 9 (mere aurii)
‎ 5 x 3 = 15 (mere roșii)
‎ 4 x 3 = 12 (banane)
‎

6. Câtul unei împărțiri este 33, iar restul 5. Să se afle deîmpărțitul, știind că împărțitorul este o treime din cât.

Rezolvare

Reconstituim împărțirea : a : b = 33 rest 5
‎ Dacă împărțitorul "b" este o treime din c ât "33" atunci b = 33 : 3 = 11
‎ Putem scrie acum împărțirea așa : a : 11 = 33 rest 5.
‎ Scriem proba împărțirii :
‎ a = 11 x 33 + 5
‎ a = 363 + 5
‎ a = 368
‎ Împărțirea reconstituită este : 368 : 11 = 33 rest 5
‎

7. Dacă adun 162 la triplul unui număr obțin 714. Să se afle numărul.

Rezolvare

Scriem problema în limbaj matematic notând numărul necunoscut cu litera "n ":
‎ 162 + 3 x n = 714
‎ 3 x n = 714 – 162 = 552 (triplul numărului)
‎ n = 552 : 3 = 184 (numărul căutat)

8. Georgiana are 15 ani. Mama ei are cu 24 de ani mai mult. Câți ani are mama Georgianei?

Rezolvare

V ârsta mamei = 15 + 24 = 39 ani

9. Află numerele necunoscute: a + 7 821 = 12 358, b – 3 121 = 7 253, 3 812 + c = 9 821.

Rezolvare

a = 12 358 – 7 821 = 4 537
‎ b = 7 253 + 3 121 = 10 374
‎ c = 9 821 – 3 812 = 6 009

10. Tatăl lui Viorel i-a cumpărat acestuia o bicicletă nouă. Știind că prețul bicicletei este de 2 499 de lei, iar tatăl a plătit la casă 3 000 de lei , să se afle valoarea restului primit de tatăl lui Viorel.

Rezolvare

a = 3 000 – 2 499 = 501 lei

11. Completați egalitățile următoare:

a) 9 – ... = 3
‎ b) 3 x 12 = ...
‎ c) 8 + ... = 8
‎ d) 18 – ... = 13
‎ e) ... + 5 = 13
‎ f) ... x 3 = 24
‎ g) 3 x 9 =
‎ h) 15 – ... = 6
‎ i) 52 : ... = 26

Rezolvare

‎ a) 9 – 6 = 3
‎ b) 3 x 12 = 36
‎ c) 8 + 0 = 8
‎ d) 18 – 5 = 13
‎ e) 8 + 5 = 13
‎ f) 8 x 3 = 24
‎ g) 3 x 9 = 27
‎ h) 15 – 9 = 6
‎ i) 52 : 2 = 26

Glume cu tâlc

Când rezolvi o problemă și ajungi la concluzia că vârsta tatălui este mai mică decât vărsta fiului...