Clasa a IV-a
Înmulțirea și împărțirea numerelor naturale
Înmulțirea
Înmulțirea unui număr natural cu un număr de o cifră
Exemplu: 4 782 x 8 = 38 256

1. Un magazin dorește să extindă oferta de carduri cadou cu încă trei carduri de valoare mai mare decât cele existente. Care credeți că ar putea fi cele trei valori dacă se respectă regula pe care o observați în imaginea de mai jos?

Regula este dublarea valorii cardului începând de la 50 lei.
Următoarele carduri pot fi de 400, 800 și 1600 lei
2. Numărul 56 aparține cărei table a înmulțirii din variantele de mai jos ?
a) tabla înmulţirii cu 2; b) tabla înmulţirii cu 3; c) tabla înmulţirii cu 7;
d) tabla înmulţirii cu 9; e) tabla înmulţirii cu 10;
c) tabla înmulţirii cu 7. Ar mai fi tabla înmulțirii cu 8 dar nu există în variantele propuse.
3. Pentrue a acoperi o suprafață pătrată cu latura de 60 cm sunt necesare 36 de plăci ceramice cu latura de 10cm. Calculați numărul de plăci ceramice (gresie) necesare pentru a acoperi suprafețe pătrate cu latura de: 100cm, 110 cm, 120 cm, 130cm și 140 cm.

U
n pătrat cu 6 plăci pe fiecare latură conține 6 x 6 = 36 plăci pe toată suprafața sa. Pentru un pătrat cu latura de 100cm avem nevoie de 10 plăci pe fiecare latură.
10 x 10 = 100
11 x 11 = 121
12 x 12 = 144
13 x 13 = 169
14 x 14 = 196
4. Efectuează, așezând numerele unele sub altele: 2310 x 9, 539 x 2, 12356 x 3.
2310x
9
_____
20790
539x
2
____
1078
12356x
3
______
37068
5. Bunica vrea să împartă câte 20 de bomboane celor 4 nepoți. De câte bomboane are nevoie?
20x
4
____
80
6. Calculează 23187 x 4 + 2314 x 7
23187 x 4 = 92748
2314 x 7 = 16198
92748 + 16198 = 108946
Înmulțirea cu 10, 100, 1000
Exemple:
5 x 10 = 50
31 x 10 = 310
La înmulțirea cu 10 se adaugă un zero la dreapta numărului.
760 x 100 = 76 000
45 x 100 = 4 500
La înmulțirea cu 100 se adaugă doup zerouri la dreapta numărului.
87 x 1 000 = 87 000
980 x 1 000 = 980 000
La
înmulțirea cu 1000 se adaugă trei zerouri la dreapta numărului.
7. Biletul la ștrand costă 10 lei de persoană. Să se calculeze costul total al biletelor pentru un grup de 50 de persoane.
10 x 50 = 500 lei
8. Un cioban dorește să își extindă stâna prin cumpărarea a 25 de oi a câte 100 de euro bucata și 10 oi care costă 250 de euro bucata. Să se afle prețul pe care îl va plăti ciobanul pentru a cumpăra toate oile.
25 x 100 = 2500
10 x 250 = 2500
2500 + 2500 = 5000 €
9. Efectuează înmulțirile: 172*10, 172*100, 172*1000.
172 x 10 = 1720
172 x 100 = 17200
172 x 1000 = 172000
Pentru a înmulți un număr cu 10, 100, 1000 adăugăm 1, 2 respectiv 3 zerouri la dreapta acelui număr.
Înmulțirea unui număr natural cu un număr de două cifre
Exemplu:

10. Efectuează următoarele înmulțiri: 12 x 12, 15 x 16, 30 x 32.
12 x 12 = 144; 15 x 16 = 240; 30 x 32 = 960
11. Prețul unui bilet de tren pe ruta Brașov-București la clasa I este de 39 de lei, iar la clasa a II-a este de 25 de lei. Să se calculeze prețul a 12 bilete la clasa I și a 17 bilete la clasa a II a, dar și costul total al acestor bilete.
12 x 39 = 468 lei este prețul biletelor de la clasa I
17 x 25 = 425 lei este prețul biletelor de la clasa a II-a
468 + 425 = 893 lei este prețul total al biletelor
12. O grădină zoologică primește 21 000 de vizitatori anual. Dacă prețul unui bilet de intrare este de 14 lei, să se afle suma totală încasată de grădina zoologică.
21 000 x 14 = 294 000
Înmulțirea a două numere naturale de 3 cifre
Exemplu: 729 x 38 = 729 x 8 + 729 x 3 x 10 = 5832 + 2187 x 10 = 27702


Brahmagupta – matematician Indian 590 – 665 d.Hr.
Prima relatare despre algoritmul de înmulțire care se bazeaza pe scrierea pozițională este din cartea lui Brahmagupta. Cartea se numește “Brahmasphutasiddhanta” (“Deschiderea spre Univers”) care a fost un mare succes în Bagdad, dup ă ce a fost tradusă în arabă. Această carte stă la temelia dezvoltării matematicii în lumea arabă și apoi în Europa.
În această carte, Brahmaghupta definește pentru prima dată numărul zero, stabilește algoritmi pentru adunare și scădere și regulile operațiilor elementare cu fracții.
Brahmaghupta descrie o cale de a face produsul a două numere de trei cifre pe care o denumește „gomutrika ” care tradusă ar însemna : “in zig-zag” sau “asem ănător cu urma lăsată de urina vacilor ”.
S ă luăm ca exemplu 321 x 457
Luăm ficare cifră și scriem valoarea ei în număr în funcție de ordinul unde se află. De exmplu din 321, 3 reprezintă 300, 2 reprezintă 20 iar 1 este doar o unitate.
Înmulțim apoi acele numere pe rând, cu al doilea număr și scriem așa :
300 x 457 = 137100
20 x 457 = 9140
1 x 457 = 457
Acum așezăm produsele astfel încât cifrele cu aceeași semnificație (din aceeași ordin) să fie așezate una sub alta : unit ăți sub unități, zeci sub zeci, sute sub sute, etc. ... Și le adunăm.
3 137100
2 9140
1 457
___________
146697
Observați cât de asemănător este acest algoritm cu cel pe care îl folosim azi chiar dacă, în cartea lui Brahmagupta zero nu era notat întotdeauna dar era totuși înlocuit cu un spațiu.
3 1371
2 914
1 457
___________
146697
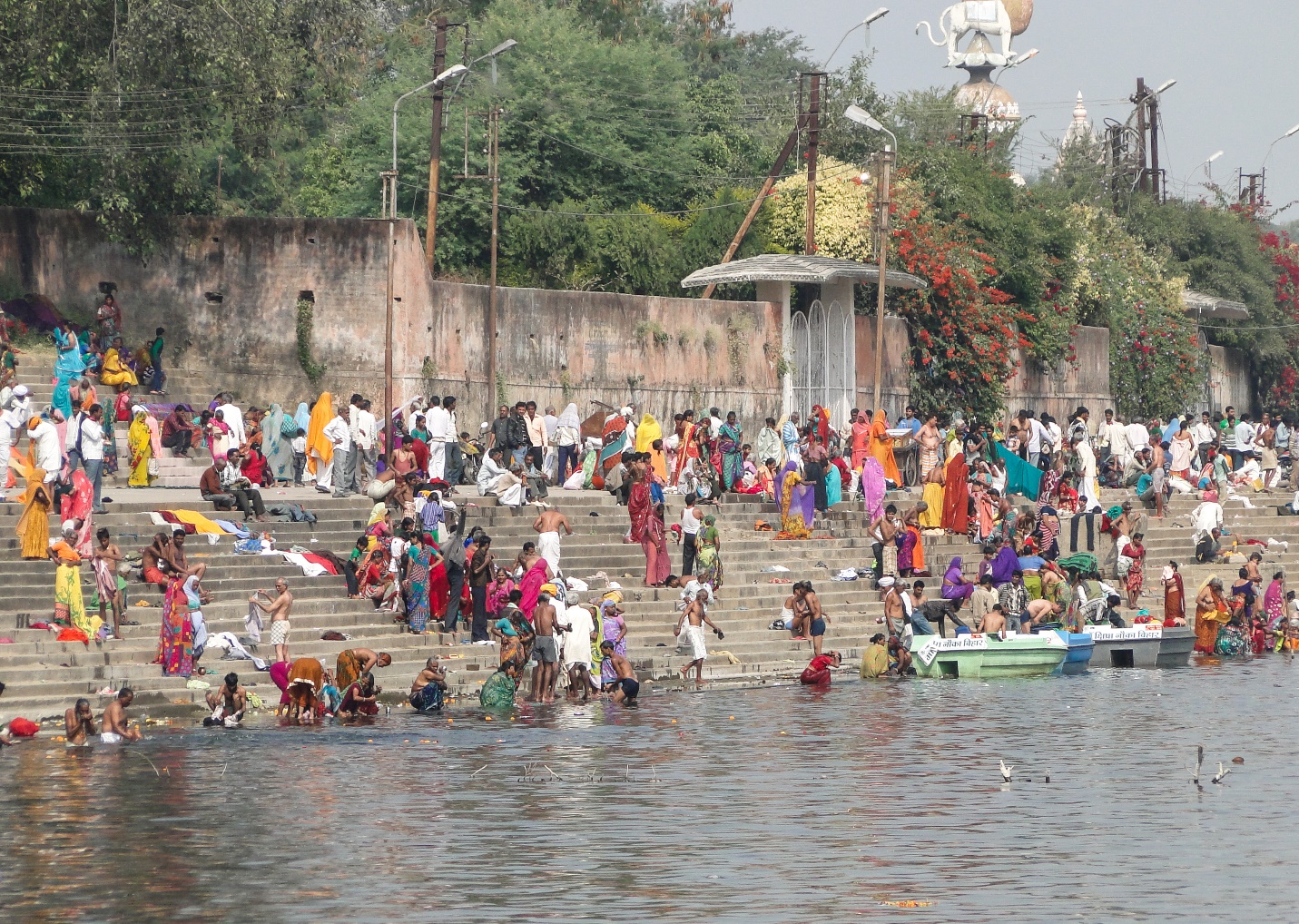
Ujain, adunare pe râul Shipra, India

Temple pe râul Kshipra, contemporane cu Brahmagupta
13. Aflați diferența dintre produsul numerelor 321 și 312 și suma lor.
321 x 312 = 100 152
321 + 312 = 6
33
100152 – 633 = 99519
14. Să se înmulțească cel mai mic număr de 3 cifre distincte cu cel mai mic număr de 3 cifre format doar din cifre pare.
102 x 200 = 20 400
15. Să se calculeze numărul x care este egal cu produsul numerelor 582 și 109.
582 x 109 = 63 438
Înmulțirea – exerciții
16. Calculează: 12 x 5 ; 8 x 16; 23 x 4.
12 x 5 = 60
8 x 16 = 128
23 x 4 = 92
17. Calculează în două moduri diferite: 8 x (5 + 7 + 1) =
8 x (5 + 7 + 1) = 8 x 13 = 104
8 x (5 + 7 + 1) = 8 x 5 + 8 x 7 + 8 x 1 = 40 + 56 + 8 = 96 + 8 = 104
18. Calculează după modelul: 15 x 7 = 10 x 7 + 5 x 7 = 70 + 35 = 105 următoarea înmulțire: 14 x 9.
14 x 9 = 10 x 9 + 4 x 9 = 90 + 36 = 126
19.
Andrei este mândru că a efectuat cea mai grea împărțire pe care a întâlnit-o până acum 3 956 172
: 5412 = 731.
Spune
tu dacă Andrei a găsit corect câtul.
Efectuăm proba împărțirii prin înmulțire. Iată un exemplu simplu
6
: 2 = 3 deci 2 x 3 = 6
3 956 172
: 5412 = 731 deci 5412 x 731 =
3 956 172. Rezolvarea lui Andrei este corectă.
20. Scrie numerele 36, 64, 108 ca produs de două numere diferite în două moduri distincte :
model: 12 = 3 x 4; 12 = 6 x 2;
36 = 12 x 3; 36 = 4 x 9
64 = 32 x 2
; 64 = 16 x 4
108 = 27 x 4; 108 = 9 x 12
21. Află numărul necunoscut : 12 x (2 + ?) = 60; 11 x (16 - ?) = 110;
12 x 2 + 12 x a = 60; 24 + 12 x a = 60;
proba adunării prin scădere
:
12 x a = 60 – 24 = 36;
proba înmulțirii prin împărțire
:
a = 36 : 12; a = 3
11 x (16 - ?) = 110; 11 x 16 – 11 x b = 110; 176 – 11 x b = 110;
proba scăderii prin scădere: 11 x b = 176 – 110 = 66; 11 x b = 66
proba înmulțirii prin împărțire: b = 66 : 11; b = 6
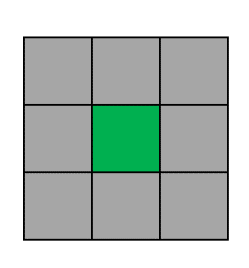
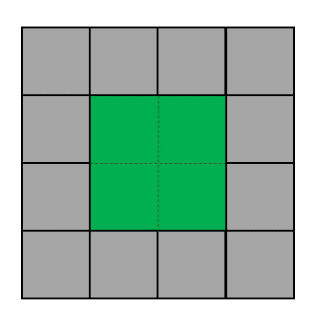
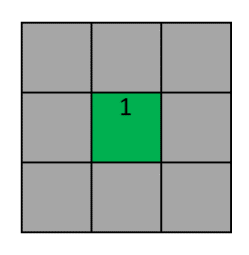
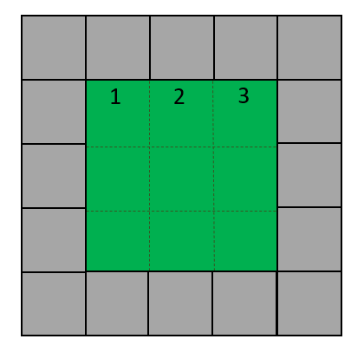
22. Dorim să împrejmuim grădina cu dale pătrate de piatră ca în figura de mai jos :
Grădina este colorată cu verde, dalele de piatră cu gri.
Grădină cu latura de o dală.
Grădină cu latura de două dale.
Grădină cu latura de trei dale.

De câte dale pătrate de piatră avem nevoie pentru a împrejmui grădina cu latura de trei dale?
Dar o grădină cu latura de 10 dale?
Care este cea mai mare grădină pe care o putem împrejmuni dacă avem doar 100 de dale pătrate?
Notăm cu N numărul de dale care încap pe o latură a grădinii.
În acest caz N = 1
În acest caz N = 2
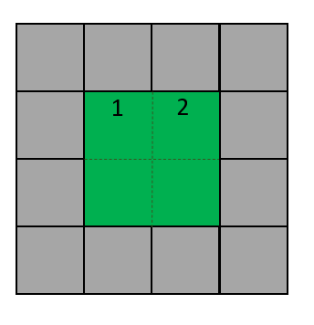
În acest caz N = 3
Numărul de dale necesare este egal 4xN + 4
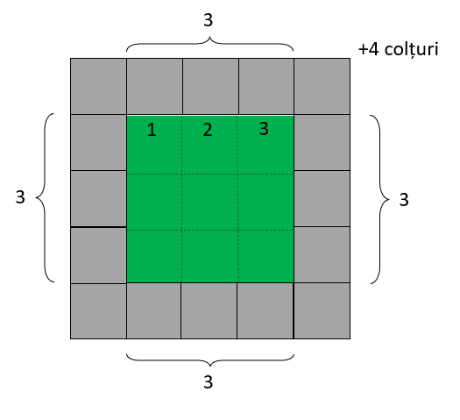
Pentru a împrejmui o grădină cu latura de 3 dale avem nevoie de 4x 3 + 4 = 12 + 4 = 16 dale.
Pentru a împrejmui o grădină cu latura de 10 dale avem nevoie de 4x 10 + 4 = 44 dale.
Cât de mare este grădina pe care o putem împrejmui cu 100 de dale?
4 x ? + 4 = 100 ?
100 – 4 = 96
96 : 4 = 24 dale.
Glume cu tâlc
Cum explicați?

Vrei să descoperi lucruri noi? Identifică personajele din imagine căutând pe Internet fizicieni celebri.
